Areas of circles and sectors quiz: Embark on an intellectual journey that will challenge your understanding of circular geometry and equip you with the skills to navigate real-world applications with precision and confidence.
Delve into the captivating world of circles and sectors, where the relationship between radius, central angle, and area unfolds, providing a solid foundation for problem-solving and critical thinking.
Circle Area and Sector Area: Areas Of Circles And Sectors Quiz
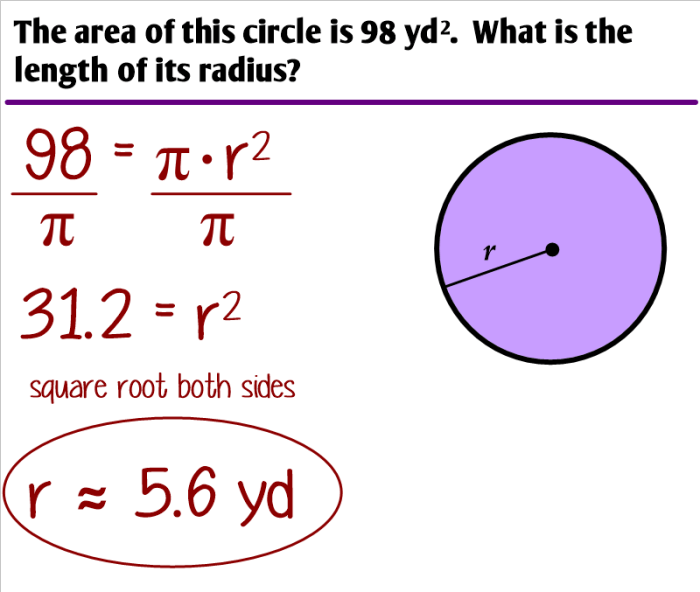
Circles and sectors are fundamental geometric shapes with applications in various fields. Understanding their areas is crucial for solving problems related to geometry, engineering, and architecture.
The area of a circle is calculated using the formula: A = πr², where ‘r’ represents the radius of the circle and ‘π’ is a mathematical constant approximately equal to 3.14.
For example, if a circle has a radius of 5 units, its area would be A = π – 5² = 25π ≈ 78.54 square units.
The relationship between the radius and the area of a circle is directly proportional. As the radius increases, the area increases at a quadratic rate.
Sector Area Formula
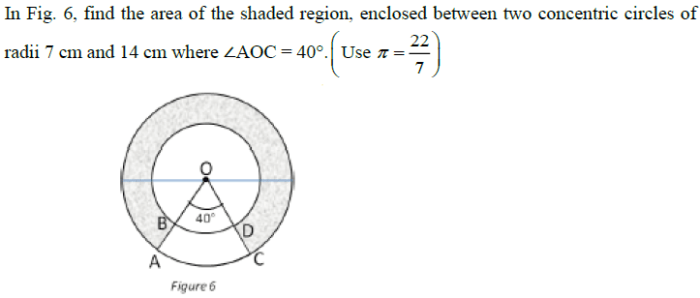
A sector is a portion of a circle enclosed by two radii and the intercepted arc. The area of a sector is calculated using the formula: A = (θ/360) – πr², where ‘θ’ represents the central angle of the sector in degrees, ‘r’ is the radius of the circle, and ‘π’ is the mathematical constant.
For instance, if a sector has a central angle of 60 degrees and a radius of 10 units, its area would be A = (60/360) – π – 10² = (1/6) – 100π ≈ 52.36 square units.
The relationship between the central angle and the area of a sector is directly proportional. As the central angle increases, the area of the sector increases proportionally.
Quiz Questions
- Calculate the area of a circle with a radius of 7 cm.
- Find the area of a sector with a central angle of 120 degrees and a radius of 5 cm.
Interactive Table, Areas of circles and sectors quiz
| Shape | Formula | Input | Result |
|---|---|---|---|
| Circle | A = πr² | Radius: | Area: |
| Sector | A = (θ/360)
|
Central Angle: Radius: | Area: |
To use the table, enter the appropriate values in the input fields and click the ‘Calculate’ button to obtain the area of the circle or sector.
Real-World Applications
- Engineering:Calculating the area of circular components, such as gears, bearings, and shafts.
- Architecture:Determining the area of circular structures, such as domes, arches, and windows.
- Design:Creating circular patterns, logos, and other design elements.
Q&A
What is the formula for calculating the area of a circle?
Area = πr², where r is the radius of the circle.
How is the area of a sector related to the central angle?
The area of a sector is proportional to the central angle. A sector with a central angle of θ degrees has an area of (θ/360)πr², where r is the radius of the circle.